要素 ( element / 元 ) の表し方 ∈ 【高校数学の集合単元から】
集合に含まれている" 要素 ( element /元 )"を表す記号に慣れておくと良いかと思います。
高校の数学から使い始めます。集合の要素を表す記号は「∈」です。
また、部分集合を表す「⊂」についても、後半の部分に書いています。
集合を A というように大文字で書き、含まれている要素を a などと小文字で書きます。
集合の要素が具体的な数字のときは、数字をそのまま書きます。
まずは、集合に含まれる要素の表し方から説明します。
要素 :集合の二つの表し方
集合に含まれているものを、要素(元)といいます。
要素を含んでいる枠組みとなる範囲の集合について、表し方が二つあるということを述べておきます。
{1, 2, 3} というように、含まれている要素を列挙して表す集合の表し方を外延的表記といいます。
※ 高校数学では学習しない用語ですが、二つの表し方を認識しやすいように、敢えて大学の数学の本に書いている言い方を書いています。
{x | x は自然数, x ≦ 3} という表し方を内包的表記といいます。条件を満たすものをすべて集めてできる集合という意味です。
今、二つの表し方について書きましたが、どちらも集合として同じものになります。
どちらの集合も {1, 2, 3} と三つの自然数を含んだ集合です。このように、同じ集合でも、二つの表し方ができるということを押さえておくのが基本となります。
敢えて、高校数学では使わない外延的表記と内包的表記という言葉を使いました。
同じ集合であっても、二つの表し方があるということを強調するために、難しそうな言葉を使いました。
というのも、名前のついていないものは、認識しにくいからです。
同じ集合でも、一つの証明の中で、外延的表記と内包的表記を両方で表されることがありますので、ご注意ください。
単純な議論のときには、誤解することはないかと思いますが、複雑な議論をしているときには注意が必要です。
同じ集合 A であっても、あるときには外延的表記で書かれていて、途中で内包的表記で表されるといったときがあります。
数学を学習するときの基本として、集合の表し方には二つの表し方があることを押さえておくと良いかと思います。
状況によって、途中でもう一つの表し方に変更されることもあるということを知っておくと良いかと思います。
それでは、集合の要素であることを表す記号「∈」の使い方について説明をしていきます。
いくつかのバリエーションがあるので、それらを書いておきます。
高校数学の表記
集合 A が {a, x, z} という三つの要素で構成されていたとします。
このときに、a という要素が、集合 A に含まれているということを次のように表します。
a が A の左側に書くときと、a が A の右側に書くときがあります。
そして、それぞれについて a が A に含まれていないという否定を表す記号があります。

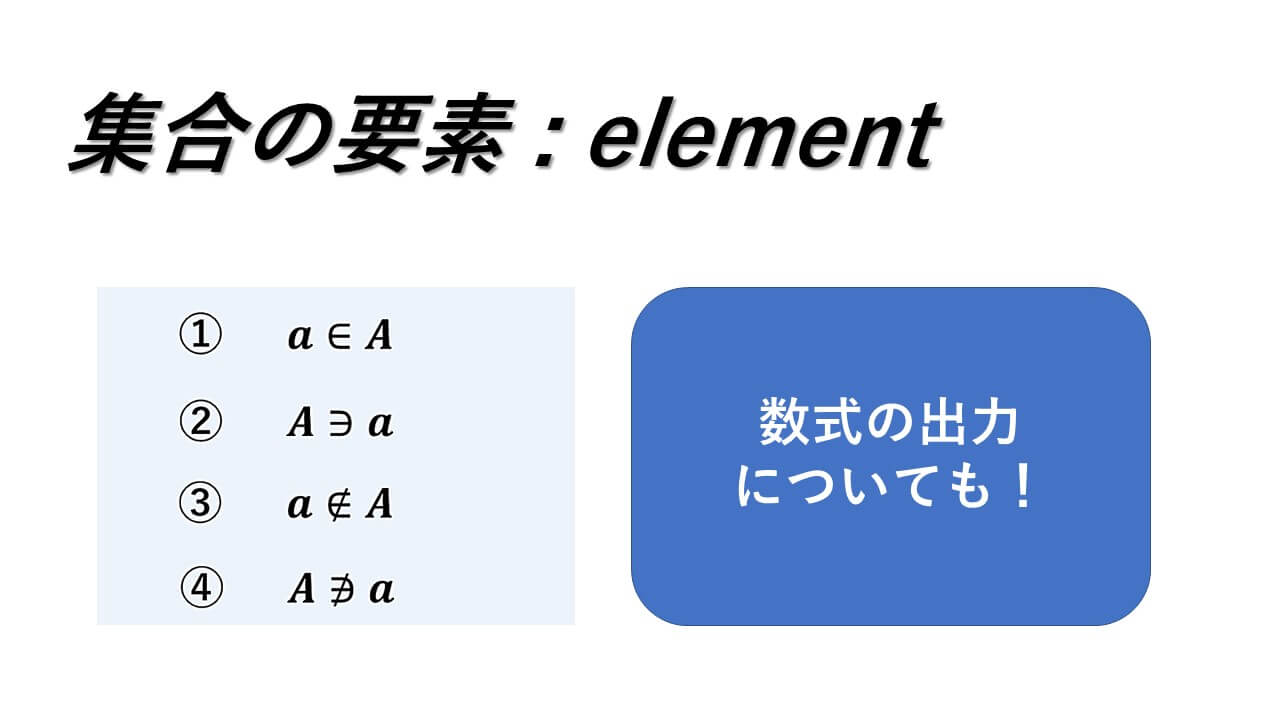
①と②は、a が集合 A の要素(元)ということを表しています。
集合 A の左側に a を書くときに①の表し方をし、集合 A の右側に a があるときには②の表し方をします。
また、a が集合 A に含まれていないということを表したいときには、③や④の表し方をします。
「∈」を否定する記号は、③や④のようにスラッシュを引きます。
※ イコールの意味を否定するときと同じく上にスラッシュを入れると押さえておくと覚えやすいかと思います。
高校数学を学習するときに、細かいですが、こういった記号の使い方を押さえておくと、正しくテキストに書かれている内容が認識できます。
また、自分が考えていることを正しく表現することができます。
a ∈ A を英語で表すと、a in A ということになります。集合という範囲内に、要素 a が含まれているということです。
a ∈ A を否定すると、a is not in A です。
大学の専門課程の数学を学習するときには、英語で書かれた本で学習することもあります。
数学を英語で表すということにも、余裕があるときに触れておくと良いかと思います。
記号を押さえる
高校1年の数学の集合の単元で「∈」を学習しますが、記号の意味や使い方を正確に押さえておくことが大切になります。
「a ∈ A」と「A ∋ a」は、同じことを意味しています。
小文字で書かれた a が、大文字で書かれた集合 A に含まれているということです。
知っていれば、なんてないことでも、知らないと意味を正しく認識できないということも起きてきます。
ですので、数学を学習するときに、記号が示す意味を正確に把握しておくことが大切になります。
あと、日本語ですが、「含まれる」ということを「属する」ということもあります。
a belongs to A ということです。
どちらも同じことを意味していますので、使っているテキストの言い方に慣れておけば大丈夫です。
ここから、部分集合について説明します。
要素 :類推で包含関係も
先ほどは、要素が集合に含まれるということを表しました。集合は大文字で表し、要素は小文字です。
今度は、大文字で書かれた集合が、大文字で書かれた集合に含まれているということを表します。
部分集合であることを表すときに、記号を間違って「∈」と書いてしまわないように注意です。
普段あまり使わない数学の記号なだけに、集合の要素であることを表す記号と部分集合である記号を正しく使えるように意識をしておくのが大切かと思います。
部分集合の記号
A ⊂ B (A は B の部分集合)
集合が集合に含まれているということについては、「⊂」を使います。
記号の左と右が、どちらも大文字になっているだけで、先ほどの「∈」のときと使い方は同様です。
「⊂」の記号の開いている方に書いている集合が、含んでいるより大きい集合ということを意味します。
※ 要素のときと同じく 「⊃」と逆転させて表すときがあります。
左の集合の方が含んでいるときには、記号の向きを逆にするだけです。
否定するときには、スラッシュを上書きするということも「∈」のときと同じです。
要素の記号と同じ要領で、部分集合の記号も習得できるので、一気に合わせて押さえておくと良いかと思います。
まとめると、集合と集合の含まれるという表し方は、「⊂」を使い、左と右に大文字で書かれた集合を配置するということです。
・開いている方に書かれている集合が含む集合。
・含む集合を左に書くときは、
逆向きに「⊃」を使う。
・否定するときは、スラッシュを上書き。
「∈」を「⊂」にして、同じ要領で使うことができます。
では、部分集合の表し方をまとめます。

①は集合 A が集合 B に含まれているということです。
②は集合 B は集合 A を含んでいるということで、①と同じ内容です。
③は集合 A は集合 B に含まれていないということで、①(もしくは②)の内容を否定したものです。
④も、③と同じ意味になります。集合 A が集合 B に含まれているときに、A は B の部分集合といいます。
A と B が一致していないときには、真部分集合といいます。
部分集合の定義
集合 A が、集合 B の部分集合であるということの定義です。
A に含まれているどの要素も、すべて集合 B に含まれているということです。
集合 A に含まれているどの要素も、すべて集合 B に含まれているということを、難しい言い方で表してみます。
「集合 A の任意の要素が、集合 B に含まれている」ということです。
数学の論理で、「任意の」という言い方が出てくるので、部分集合の定義を通じて押さえておくと、合わせて理解しやすいかと思います。
真部分集合についても、さらに深く定義について説明をします。集合 A が集合 B の真部分集合であるとき、集合 A に含まれている要素は、どれも集合 B に含まれています。
しかし、集合 A と集合 B は一致していません。つまり、集合 A が集合 B の真部分集合であるとき、集合 B の要素で、集合 A には含まれていないものが存在するということになります。
部分集合の具体例
A = {1, 2}, B = {1, 2, 3} について、
A ⊂ B となっています。
そして、A は B の真部分集合です。
定義の内容を確認します。集合 A に含まれているどの要素も、集合 B に含まれているので、A は B の部分集合です。
「1 ∈ A 、1 ∈ B」ですし、
「2 ∈ A は、2 ∈ B」となっています。
確かに集合 A の要素は、すべて集合 B に含まれています。
真部分集合と言い切れるのは、3 ∈ B が存在するからです。
3 は集合 B に含まれていますが、集合 A に含まれていません。
数学で新しい単元を学習するときには、まず定義に当てはまるかどうかを確認することからスタートすると、理解しやすいです。
要素 :数学の学習について
具体例を通じて、定義に当てはまるか、当てはまらないかを確認すると、様子が段々と分かってきて、数学の用語の理解が深まっていきます。
また、具体的に書いてみると、より分かりやすくなるかもしれません。
例えば、An という自然数 n に応じて定まる集合があったとします。
それぞれの自然数 n について、どういう要素が、その集合に含まれているのかを確認します。
{x | x は自然数, 5n ≦ x ≦ 6n}
= An
この条件を満たすものたちが、要素として集合に含まれます。
これは、はじめに与えられた自然数 n に応じて定まる集合です。
自然数 n が 3 のときだと、15 以上 18 以下の自然数が含まれるということになります。
A3 には、15, 16, 17, 18 が含まれることになります。
ところが、n = 2 だと、10 ≦ x ≦ 12 となります。A2 には 10, 11, 12 が含まれるということになります。
このように、はじめに与えられた n の値に応じて、An に含まれる要素が変化する可能性があります。
要素(元)の注意
大学数学で学習する行列ですが、行列については、集合の要素でも大文字で表します。
行列 A というようにいつも書いているのですが、行列を集めた集合を考えるときもあります。
例えば、M(2, R) を実数を成分とする 2 次正方行列全体からできている集合とします。
この集合の要素は行列なので、大文字で表されます。A ∈ M(2, R) という表し方になります。
高校数学では、集合の要素は小文字で表しているので、違和感があるかもしれません。しかし、大学数学になると、このようなものも出てきます。
ここまでの内容で、集合に含まれる要素の表し方を説明しました。高校数学で、不等式を満たす実数の範囲を集合で表すことがあります。
不等式を満たす範囲を集合で表すことによって、集合算を使えたりして、より扱いやすくなります。
とりあえずは、共通部分や和集合と関連させて押さえておくことが良いかと思います。
余裕が出てきたら、集合算を使えるようにチャレンジしてみるという流れになります。
次の内容は、高校のテストなどで出てきそうな論理的な内容です。
出題者が定義する記号も
数学では、問題を作る出題者が記号を問題の中で定義することがあります。
そのようなときには、定義に基づいて、どのように運用できるのかということを考えることになります。
試しに教科書に載っていないような記号を、このページ限定で定めてみます。
自然数 n に対して、
n の正の約数全体を nS と表すことにします。
このような知らない抽象的な記号が出てきたら、具体的なシンプルな例で様子を見ると内容が分かってくるかと思います。
例えば、4 という自然数だと、4S は 4 の正の約数全体から成る集合です。
4S = {1, 2, 4} は外延的表記で表したものです。少ない要素の集合だと、明確に表せる表記です。
ただ、具体的なもので敢えて文字を使って一般的に表すということも数学の良い練習になるかと思います。
そんな練習に次の問題を用意しました。
【問題】
6S と 8S のどちらの集合にも含まれている要素は、必ず 14S に含まれていることを確認してください。
敢えて文字を使って、示してみます。
x ∈ 6S であり x ∈ 8S だとします。
x は 4 の正の約数であり、しかも 8 の正の約数でもあるということです。
この x が 14S に含まれるということを示すには、x が 14 の正の約数であることを示せば良いということになります。
x は 6 の正の約数なので、
6 = xk (k は自然数) と表すことができます。
さらに x は 8 の正の約数でもあるので、
8 = xt (t は自然数) と表すことができます。
連立方程式の加減法の要領で、二つの等式を辺々足し合わせてみます。
なぜ足すかというと、6 + 8 = 14 だからです。
そして、
14 = xk + xt = x(k + t) です。
ここで、k + t は自然数ですから、x が 14 の正の約数ということを意味しています。
x が 14 の正の約数ということは、x ∈ 14S ということです。
ちなみに、内包的表記で 14S を表すと、
14S = {y | y は14 の正の約数}
「14 = x × 自然数」となっている正の整数 x は、14 の正の約数なので、この集合に含まれるための条件に当てはまっているということになります。
次の内容は、少し発展的な内容ですが、高校の定期考査などでよく出てくる内容です。
要素 :有限集合の部分集合が何個あるか
大学の数学で、集合 X について、X の部分集合をすべて集めたベキ集合という集合族を扱います。
高校数学では、この名前は出てきません。
しかし、有限集合のベキ集合が何個あるのかを数える問題がテストなどで出題されたりします。
X = {1, 2, 3} という三点集合について、ベキ集合を構成する X のすべての部分集合を求めてみます。
X の部分集合 Y を作るときに、次の判断をします。「X のそれぞれの要素について、Y の要素とするか、それとも Y の要素としないか」という判断です。
論理的に数え上げると、次の 8 通りの X の部分集合の作り方があります。
Y の要素とするとき 〇, Y の要素としないとき × と表すことにします。
[1] 1×2×3×, [2] 1×2×3〇,
[3] 1×2〇3×, [4] 1×2〇3〇,
[5] 1〇2×3×, [6] 1〇2×3〇,
[7] 1〇2〇3×, [8] 1〇2〇3〇
これらの中で極端なのが、[1] と [8] です。[1] のときには、Y には一つの要素も無いので、Y は空集合 Φ です。
また、[8] は X の要素をすべて含んでいるため、Y は X 自身となっています。
他のときは、[7] だと 1 と 2 を Y の要素としているので、Y = {1, 2} ⊂ X という真部分集合になっています。
数式の入力
このブログで、集合に要素が含まれることを表す記号と、部分集合を表す記号について説明しました。
大学の数学科の方は、卒業論文でtex(数式入力)が必須になる場合もあるかと思います。
リンク先の記事でも、入力の仕方についての内容を説明しています。
手書きではよく書いている記号だけれども、どういうソースコードを入力すれば良いのか知らないということもあるかと思います。
昔の私が、数式を入力するときに、含まれているという記号を逆向きに出力する方法を知らなくて、調べたことがありました。
やり始めのときには、このようなことはよくあるかと思います。そこで、記号の入力について書いておきます。
「∈, ∋」についての入力です。
\in と入力します。逆向きの記号は\ni となります。
in を逆向きにすると、記号が反対と覚えておくと良いかと思います。
※ バックスラッシュは、入力するときに半角英数字でご入力ください。
「⊂, ⊃」についての入力です。
この記号の入力も、なぞなぞのようなものです。
\subset の b をアップサイドダウンでひっくり返し p にします。
そうすると逆向きに出力されます。\supset は上下逆さまで、部分集合の向きが逆転します。

卒業論文で、数式入力が必須になる場合には、早い目に入力方法に慣れておくことが大切かと思います。
Java などに関連する内容を変更するといったようなことまではさておき、数式を出力する命令文は、大抵はシンプルなものが多いです。
分数指数という記事で、実践的な数式入力について説明をしています。
これで、今回の記事を終了します。
読んで頂き、ありがとうございました。